- Download Price:
- Free
- Size:
- 0.03 MB
- Operating Systems:
- Directory:
- A
- Downloads:
- 918 times.
Acdcp.dll Explanation
The Acdcp.dll file is 0.03 MB. The download links for this file are clean and no user has given any negative feedback. From the time it was offered for download, it has been downloaded 918 times.
Table of Contents
- Acdcp.dll Explanation
- Operating Systems Compatible with the Acdcp.dll File
- How to Download Acdcp.dll
- How to Fix Acdcp.dll Errors?
- Method 1: Copying the Acdcp.dll File to the Windows System Folder
- Method 2: Copying The Acdcp.dll File Into The Software File Folder
- Method 3: Doing a Clean Install of the software That Is Giving the Acdcp.dll Error
- Method 4: Solving the Acdcp.dll Error using the Windows System File Checker (sfc /scannow)
- Method 5: Getting Rid of Acdcp.dll Errors by Updating the Windows Operating System
- Our Most Common Acdcp.dll Error Messages
- Dll Files Similar to Acdcp.dll
Operating Systems Compatible with the Acdcp.dll File
How to Download Acdcp.dll
- Click on the green-colored "Download" button on the top left side of the page.
Step 1:Download process of the Acdcp.dll file's - After clicking the "Download" button at the top of the page, the "Downloading" page will open up and the download process will begin. Definitely do not close this page until the download begins. Our site will connect you to the closest DLL Downloader.com download server in order to offer you the fastest downloading performance. Connecting you to the server can take a few seconds.
How to Fix Acdcp.dll Errors?
ATTENTION! Before starting the installation, the Acdcp.dll file needs to be downloaded. If you have not downloaded it, download the file before continuing with the installation steps. If you don't know how to download it, you can immediately browse the dll download guide above.
Method 1: Copying the Acdcp.dll File to the Windows System Folder
- The file you will download is a compressed file with the ".zip" extension. You cannot directly install the ".zip" file. Because of this, first, double-click this file and open the file. You will see the file named "Acdcp.dll" in the window that opens. Drag this file to the desktop with the left mouse button. This is the file you need.
Step 1:Extracting the Acdcp.dll file from the .zip file - Copy the "Acdcp.dll" file you extracted and paste it into the "C:\Windows\System32" folder.
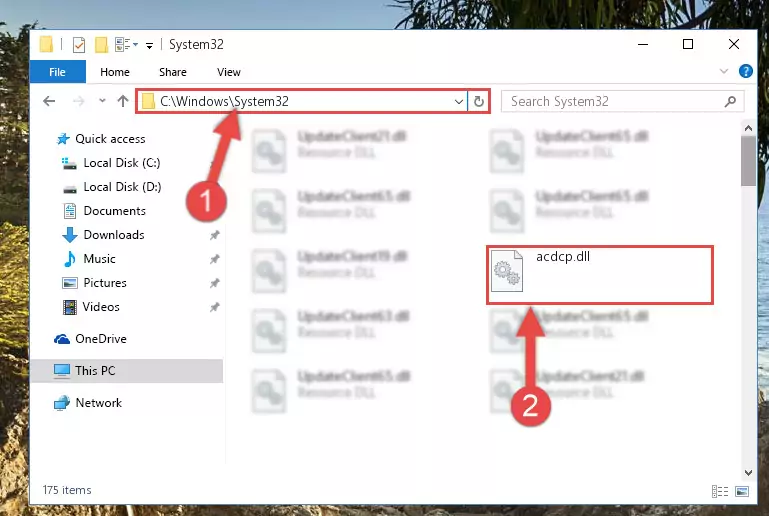
Step 2:Copying the Acdcp.dll file into the Windows/System32 folder - If your system is 64 Bit, copy the "Acdcp.dll" file and paste it into "C:\Windows\sysWOW64" folder.
NOTE! On 64 Bit systems, you must copy the dll file to both the "sysWOW64" and "System32" folders. In other words, both folders need the "Acdcp.dll" file.
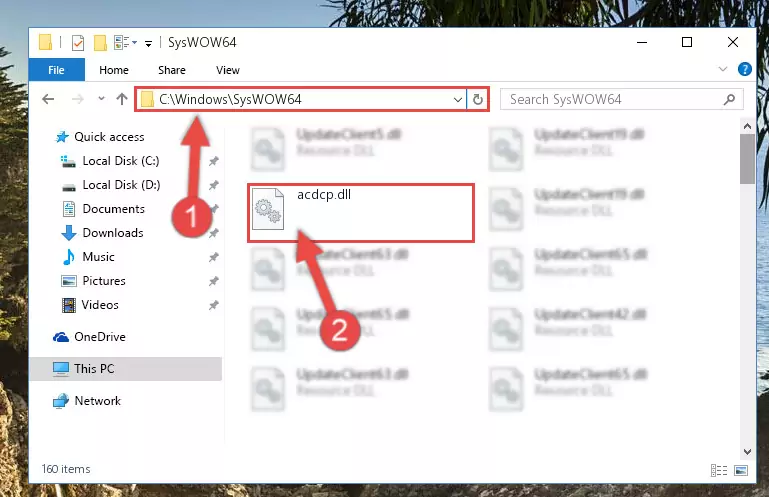
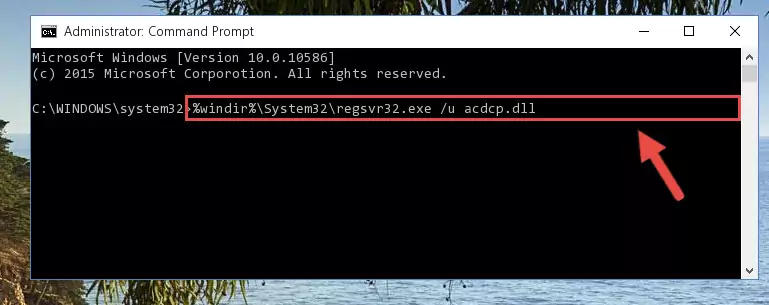
Step 3:Copying the Acdcp.dll file to the Windows/sysWOW64 folder - First, we must run the Windows Command Prompt as an administrator.
NOTE! We ran the Command Prompt on Windows 10. If you are using Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP, you can use the same methods to run the Command Prompt as an administrator.
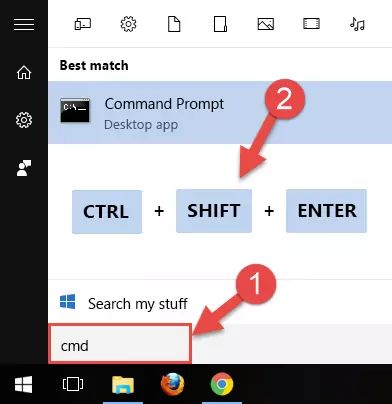
- Open the Start Menu and type in "cmd", but don't press Enter. Doing this, you will have run a search of your computer through the Start Menu. In other words, typing in "cmd" we did a search for the Command Prompt.
- When you see the "Command Prompt" option among the search results, push the "CTRL" + "SHIFT" + "ENTER " keys on your keyboard.
- A verification window will pop up asking, "Do you want to run the Command Prompt as with administrative permission?" Approve this action by saying, "Yes".
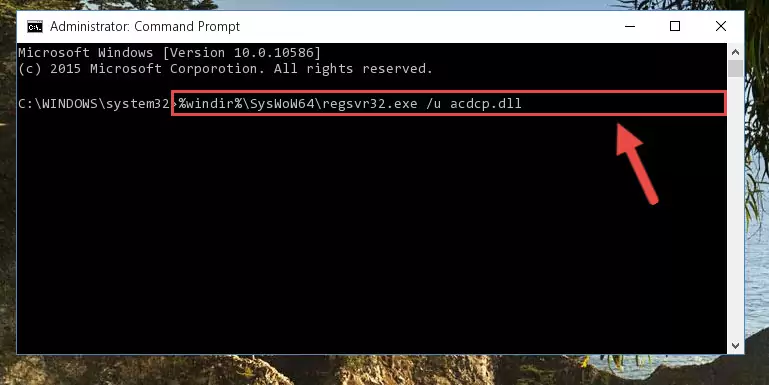
%windir%\System32\regsvr32.exe /u Acdcp.dll
%windir%\SysWoW64\regsvr32.exe /u Acdcp.dll
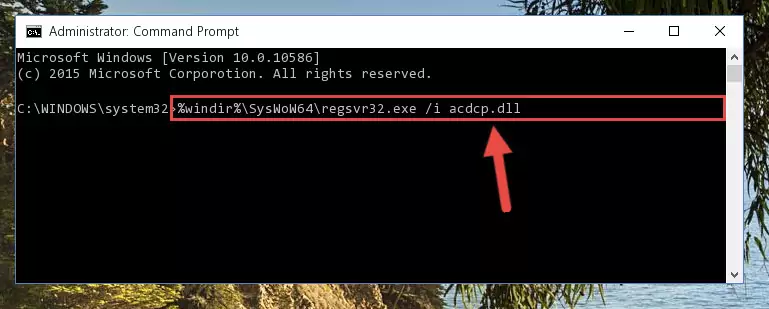
%windir%\System32\regsvr32.exe /i Acdcp.dll
%windir%\SysWoW64\regsvr32.exe /i Acdcp.dll
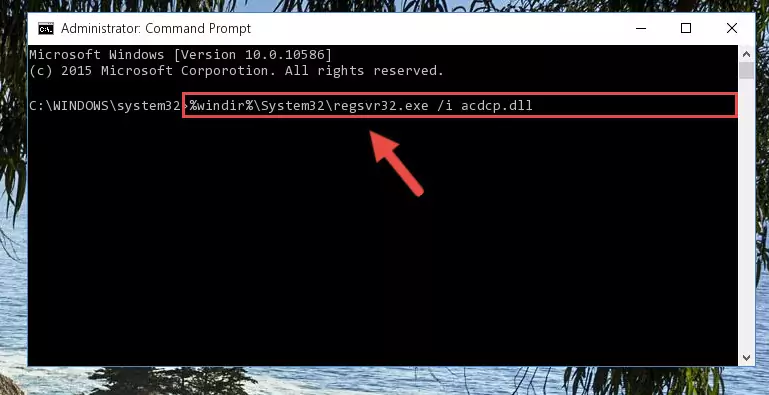
Method 2: Copying The Acdcp.dll File Into The Software File Folder
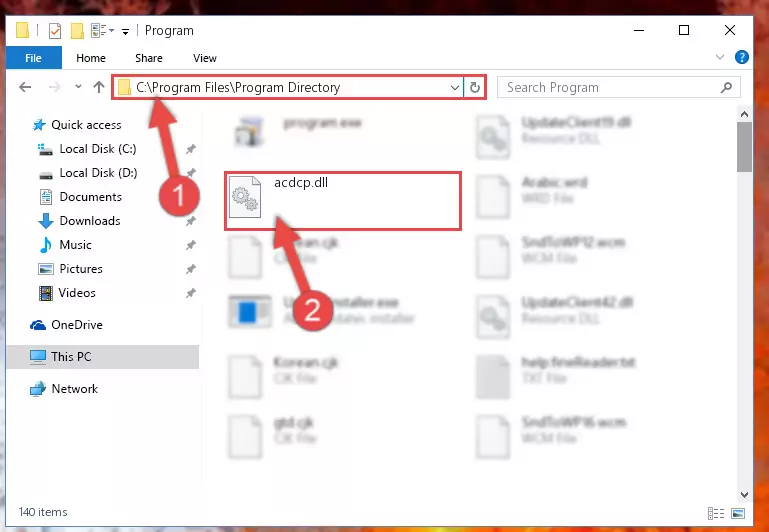
- In order to install the dll file, you need to find the file folder for the software that was giving you errors such as "Acdcp.dll is missing", "Acdcp.dll not found" or similar error messages. In order to do that, Right-click the software's shortcut and click the Properties item in the right-click menu that appears.
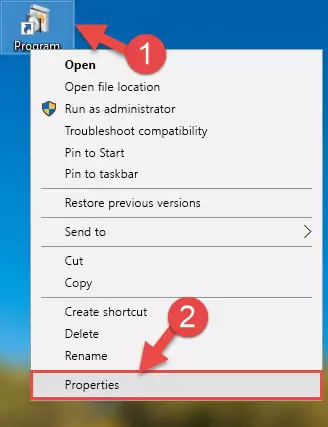
Step 1:Opening the software shortcut properties window - Click on the Open File Location button that is found in the Properties window that opens up and choose the folder where the application is installed.
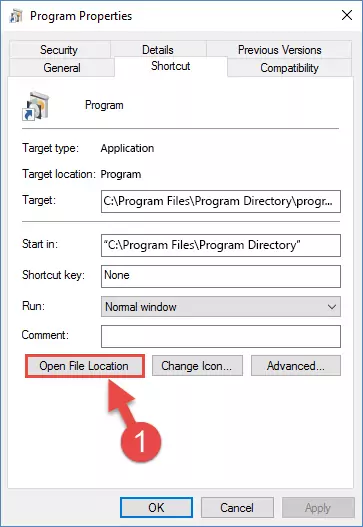
Step 2:Opening the file folder of the software - Copy the Acdcp.dll file into this folder that opens.
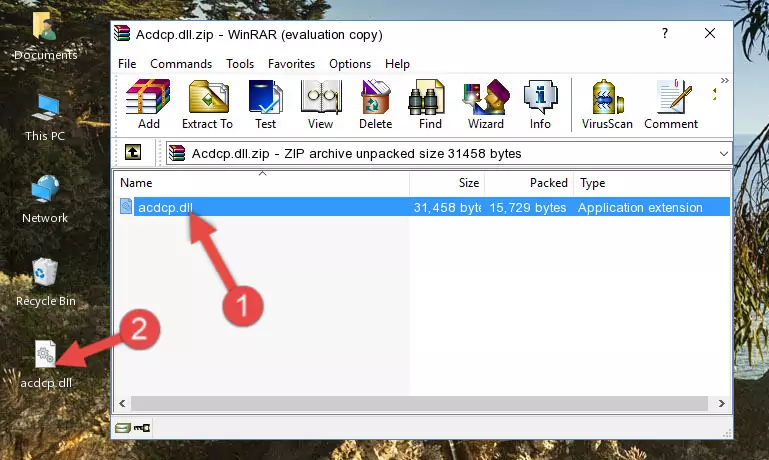
Step 3:Copying the Acdcp.dll file into the software's file folder - This is all there is to the process. Now, try to run the software again. If the problem still is not solved, you can try the 3rd Method.
Method 3: Doing a Clean Install of the software That Is Giving the Acdcp.dll Error
- Push the "Windows" + "R" keys at the same time to open the Run window. Type the command below into the Run window that opens up and hit Enter. This process will open the "Programs and Features" window.
appwiz.cpl
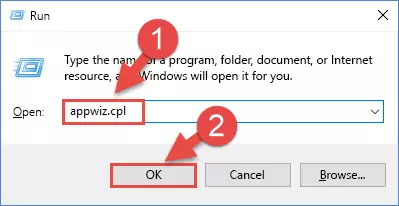
Step 1:Opening the Programs and Features window using the appwiz.cpl command - The Programs and Features window will open up. Find the software that is giving you the dll error in this window that lists all the softwares on your computer and "Right-Click > Uninstall" on this software.
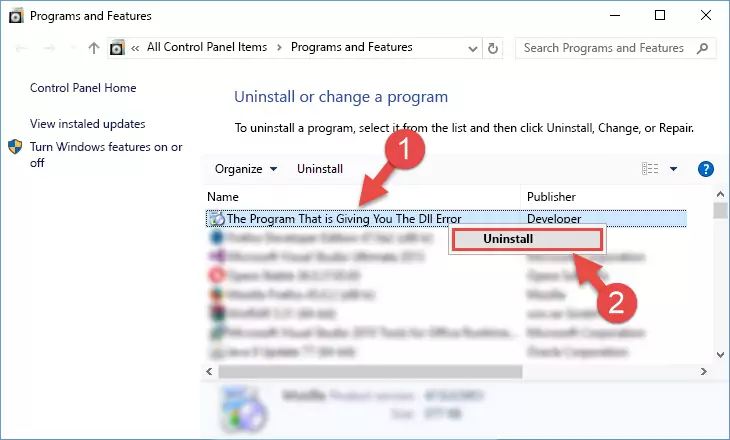
Step 2:Uninstalling the software that is giving you the error message from your computer. - Uninstall the software from your computer by following the steps that come up and restart your computer.
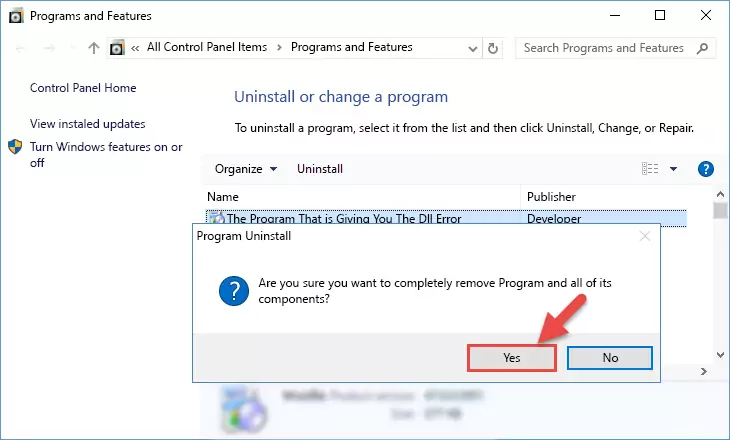
Step 3:Following the confirmation and steps of the software uninstall process - After restarting your computer, reinstall the software.
- This process may help the dll problem you are experiencing. If you are continuing to get the same dll error, the problem is most likely with Windows. In order to fix dll problems relating to Windows, complete the 4th Method and 5th Method.
Method 4: Solving the Acdcp.dll Error using the Windows System File Checker (sfc /scannow)
- First, we must run the Windows Command Prompt as an administrator.
NOTE! We ran the Command Prompt on Windows 10. If you are using Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP, you can use the same methods to run the Command Prompt as an administrator.
- Open the Start Menu and type in "cmd", but don't press Enter. Doing this, you will have run a search of your computer through the Start Menu. In other words, typing in "cmd" we did a search for the Command Prompt.
- When you see the "Command Prompt" option among the search results, push the "CTRL" + "SHIFT" + "ENTER " keys on your keyboard.
- A verification window will pop up asking, "Do you want to run the Command Prompt as with administrative permission?" Approve this action by saying, "Yes".

sfc /scannow
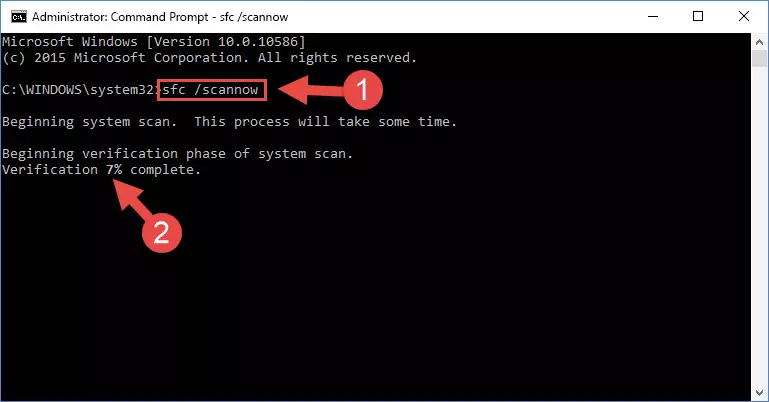
Method 5: Getting Rid of Acdcp.dll Errors by Updating the Windows Operating System
Some softwares need updated dll files. When your operating system is not updated, it cannot fulfill this need. In some situations, updating your operating system can solve the dll errors you are experiencing.
In order to check the update status of your operating system and, if available, to install the latest update packs, we need to begin this process manually.
Depending on which Windows version you use, manual update processes are different. Because of this, we have prepared a special article for each Windows version. You can get our articles relating to the manual update of the Windows version you use from the links below.
Explanations on Updating Windows Manually
Our Most Common Acdcp.dll Error Messages
The Acdcp.dll file being damaged or for any reason being deleted can cause softwares or Windows system tools (Windows Media Player, Paint, etc.) that use this file to produce an error. Below you can find a list of errors that can be received when the Acdcp.dll file is missing.
If you have come across one of these errors, you can download the Acdcp.dll file by clicking on the "Download" button on the top-left of this page. We explained to you how to use the file you'll download in the above sections of this writing. You can see the suggestions we gave on how to solve your problem by scrolling up on the page.
- "Acdcp.dll not found." error
- "The file Acdcp.dll is missing." error
- "Acdcp.dll access violation." error
- "Cannot register Acdcp.dll." error
- "Cannot find Acdcp.dll." error
- "This application failed to start because Acdcp.dll was not found. Re-installing the application may fix this problem." error
