- Download Price:
- Free
- Versions:
- Size:
- 0.12 MB
- Operating Systems:
- Developers:
- Directory:
- T
- Downloads:
- 430 times.
Tipp377.dll Explanation
The Tipp377.dll file is a dynamic link library developed by Jorg Dohler Softwareentwicklung. This library includes important functions that may be needed by softwares, games or other basic Windows tools.
The size of this dll file is 0.12 MB and its download links are healthy. It has been downloaded 430 times already.
Table of Contents
- Tipp377.dll Explanation
- Operating Systems Compatible with the Tipp377.dll File
- All Versions of the Tipp377.dll File
- Guide to Download Tipp377.dll
- Methods for Solving Tipp377.dll
- Method 1: Solving the DLL Error by Copying the Tipp377.dll File to the Windows System Folder
- Method 2: Copying The Tipp377.dll File Into The Software File Folder
- Method 3: Doing a Clean Reinstall of the Software That Is Giving the Tipp377.dll Error
- Method 4: Solving the Tipp377.dll Error using the Windows System File Checker (sfc /scannow)
- Method 5: Fixing the Tipp377.dll Error by Manually Updating Windows
- Our Most Common Tipp377.dll Error Messages
- Dll Files Similar to the Tipp377.dll File
Operating Systems Compatible with the Tipp377.dll File
All Versions of the Tipp377.dll File
The last version of the Tipp377.dll file is the 1.0.0.0 version.This dll file only has one version. There is no other version that can be downloaded.
- 1.0.0.0 - 32 Bit (x86) Download directly this version
Guide to Download Tipp377.dll
- First, click on the green-colored "Download" button in the top left section of this page (The button that is marked in the picture).
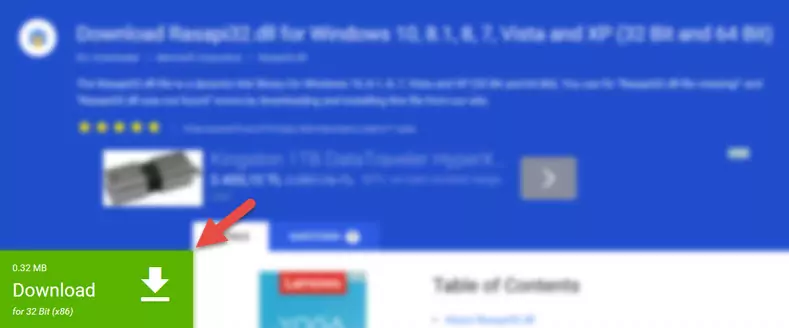
Step 1:Start downloading the Tipp377.dll file - The downloading page will open after clicking the Download button. After the page opens, in order to download the Tipp377.dll file the best server will be found and the download process will begin within a few seconds. In the meantime, you shouldn't close the page.
Methods for Solving Tipp377.dll
ATTENTION! Before starting the installation, the Tipp377.dll file needs to be downloaded. If you have not downloaded it, download the file before continuing with the installation steps. If you don't know how to download it, you can immediately browse the dll download guide above.
Method 1: Solving the DLL Error by Copying the Tipp377.dll File to the Windows System Folder
- The file you downloaded is a compressed file with the ".zip" extension. In order to install it, first, double-click the ".zip" file and open the file. You will see the file named "Tipp377.dll" in the window that opens up. This is the file you need to install. Drag this file to the desktop with your mouse's left button.
Step 1:Extracting the Tipp377.dll file - Copy the "Tipp377.dll" file file you extracted.
- Paste the dll file you copied into the "C:\Windows\System32" folder.
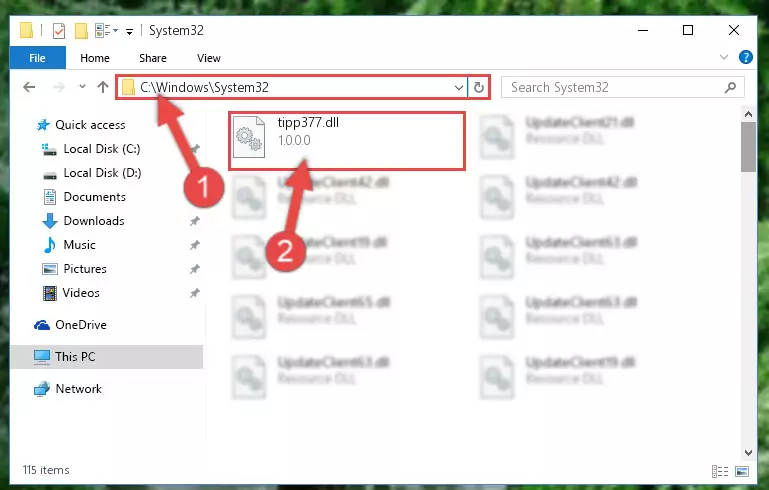
Step 3:Pasting the Tipp377.dll file into the Windows/System32 folder - If your operating system has a 64 Bit architecture, copy the "Tipp377.dll" file and paste it also into the "C:\Windows\sysWOW64" folder.
NOTE! On 64 Bit systems, the dll file must be in both the "sysWOW64" folder as well as the "System32" folder. In other words, you must copy the "Tipp377.dll" file into both folders.
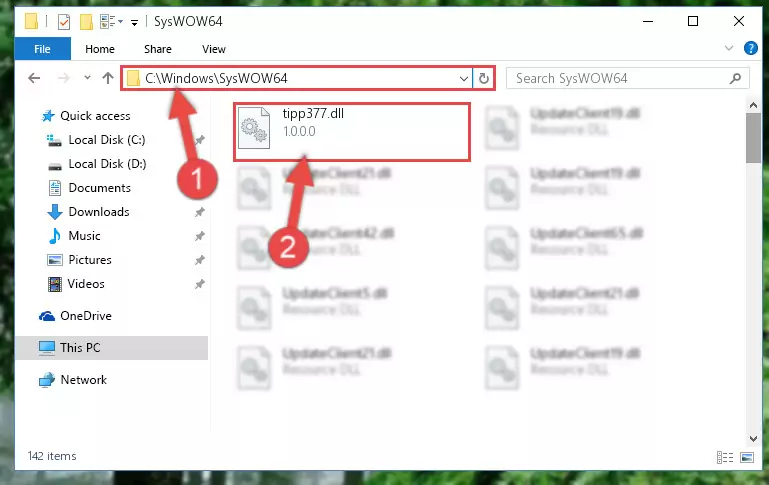
Step 4:Pasting the Tipp377.dll file into the Windows/sysWOW64 folder - First, we must run the Windows Command Prompt as an administrator.
NOTE! We ran the Command Prompt on Windows 10. If you are using Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP, you can use the same methods to run the Command Prompt as an administrator.
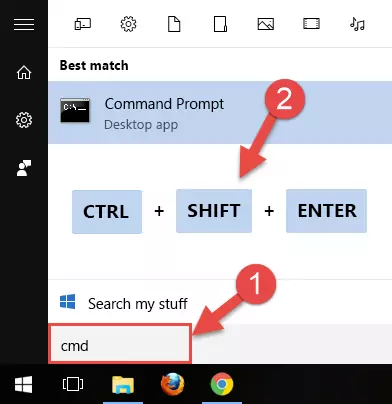
- Open the Start Menu and type in "cmd", but don't press Enter. Doing this, you will have run a search of your computer through the Start Menu. In other words, typing in "cmd" we did a search for the Command Prompt.
- When you see the "Command Prompt" option among the search results, push the "CTRL" + "SHIFT" + "ENTER " keys on your keyboard.
- A verification window will pop up asking, "Do you want to run the Command Prompt as with administrative permission?" Approve this action by saying, "Yes".
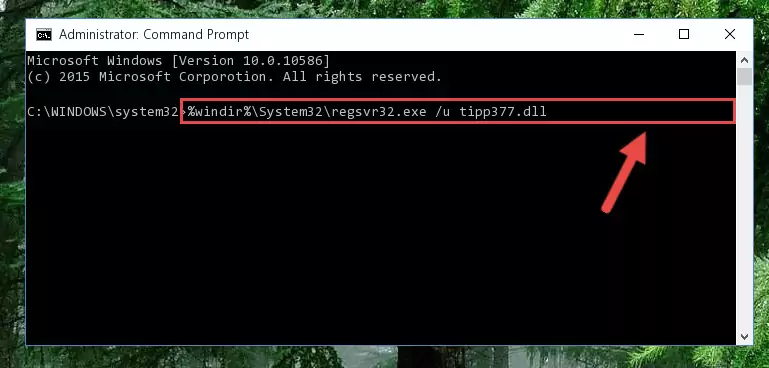
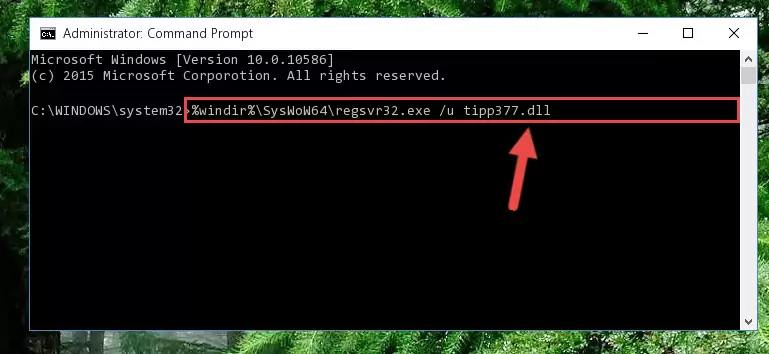
%windir%\System32\regsvr32.exe /u Tipp377.dll
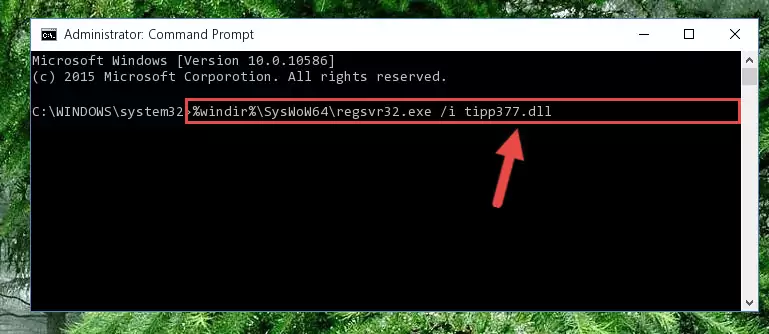
%windir%\SysWoW64\regsvr32.exe /u Tipp377.dll
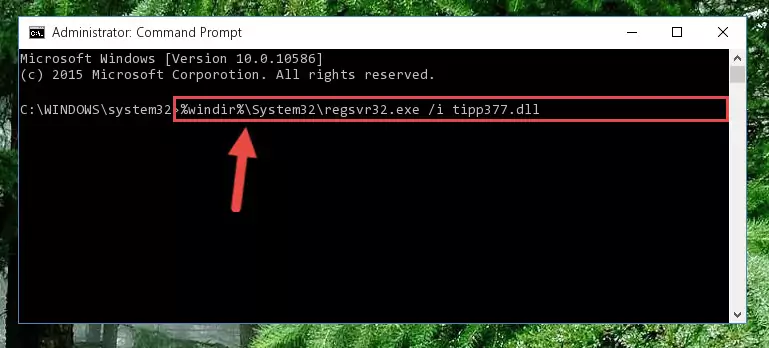
%windir%\System32\regsvr32.exe /i Tipp377.dll
%windir%\SysWoW64\regsvr32.exe /i Tipp377.dll
Method 2: Copying The Tipp377.dll File Into The Software File Folder
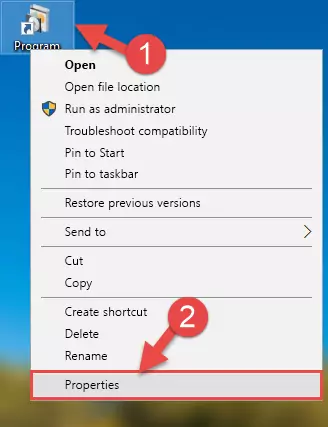
- In order to install the dll file, you need to find the file folder for the software that was giving you errors such as "Tipp377.dll is missing", "Tipp377.dll not found" or similar error messages. In order to do that, Right-click the software's shortcut and click the Properties item in the right-click menu that appears.
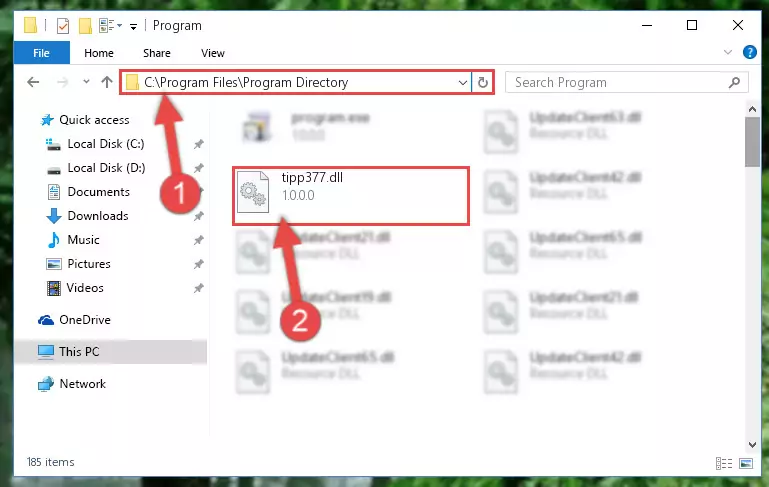
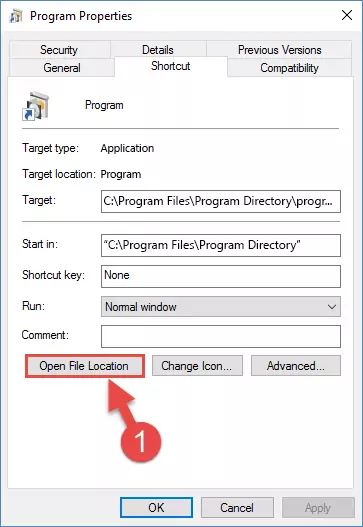
Step 1:Opening the software shortcut properties window - Click on the Open File Location button that is found in the Properties window that opens up and choose the folder where the application is installed.
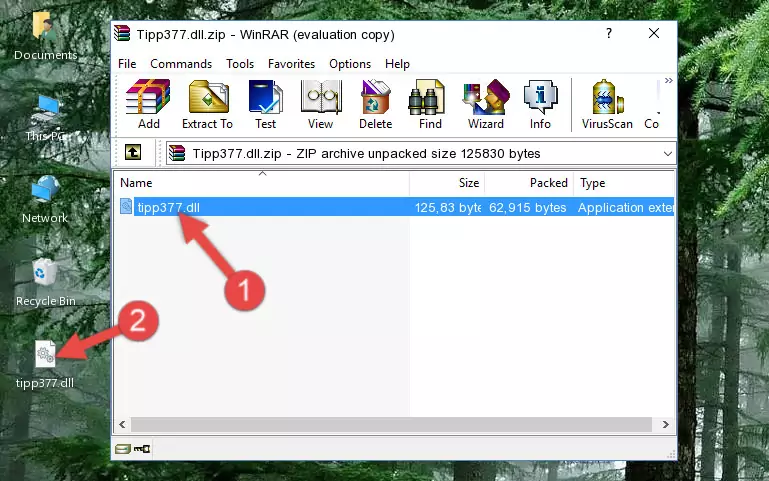
Step 2:Opening the file folder of the software - Copy the Tipp377.dll file.
- Paste the dll file you copied into the software's file folder that we just opened.
Step 3:Pasting the Tipp377.dll file into the software's file folder - When the dll file is moved to the software file folder, it means that the process is completed. Check to see if the problem was solved by running the software giving the error message again. If you are still receiving the error message, you can complete the 3rd Method as an alternative.
Method 3: Doing a Clean Reinstall of the Software That Is Giving the Tipp377.dll Error
- Open the Run window by pressing the "Windows" + "R" keys on your keyboard at the same time. Type in the command below into the Run window and push Enter to run it. This command will open the "Programs and Features" window.
appwiz.cpl
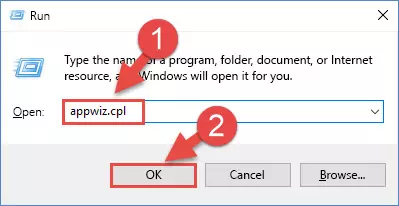
Step 1:Opening the Programs and Features window using the appwiz.cpl command - The softwares listed in the Programs and Features window that opens up are the softwares installed on your computer. Find the software that gives you the dll error and run the "Right-Click > Uninstall" command on this software.
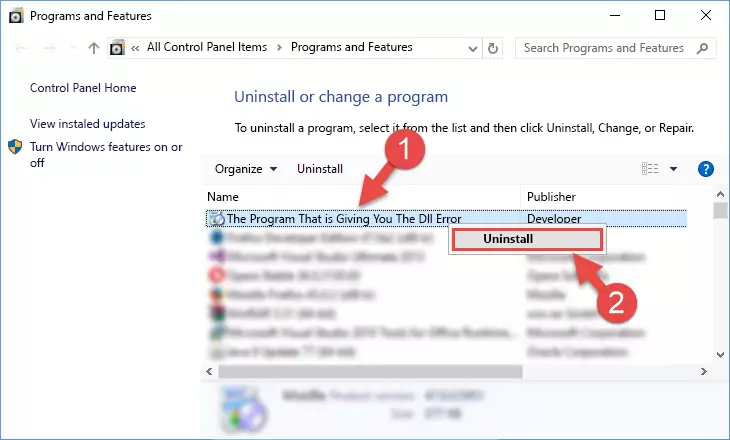
Step 2:Uninstalling the software from your computer - Following the instructions that come up, uninstall the software from your computer and restart your computer.
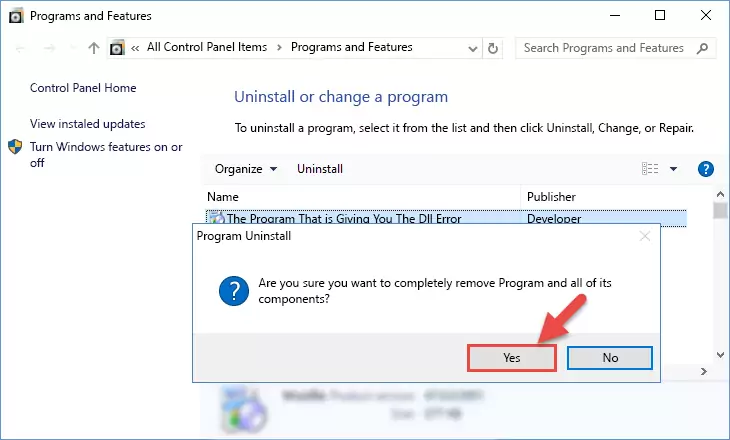
Step 3:Following the verification and instructions for the software uninstall process - After restarting your computer, reinstall the software.
- This method may provide the solution to the dll error you're experiencing. If the dll error is continuing, the problem is most likely deriving from the Windows operating system. In order to fix dll errors deriving from the Windows operating system, complete the 4th Method and the 5th Method.
Method 4: Solving the Tipp377.dll Error using the Windows System File Checker (sfc /scannow)
- First, we must run the Windows Command Prompt as an administrator.
NOTE! We ran the Command Prompt on Windows 10. If you are using Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP, you can use the same methods to run the Command Prompt as an administrator.
- Open the Start Menu and type in "cmd", but don't press Enter. Doing this, you will have run a search of your computer through the Start Menu. In other words, typing in "cmd" we did a search for the Command Prompt.
- When you see the "Command Prompt" option among the search results, push the "CTRL" + "SHIFT" + "ENTER " keys on your keyboard.
- A verification window will pop up asking, "Do you want to run the Command Prompt as with administrative permission?" Approve this action by saying, "Yes".

sfc /scannow
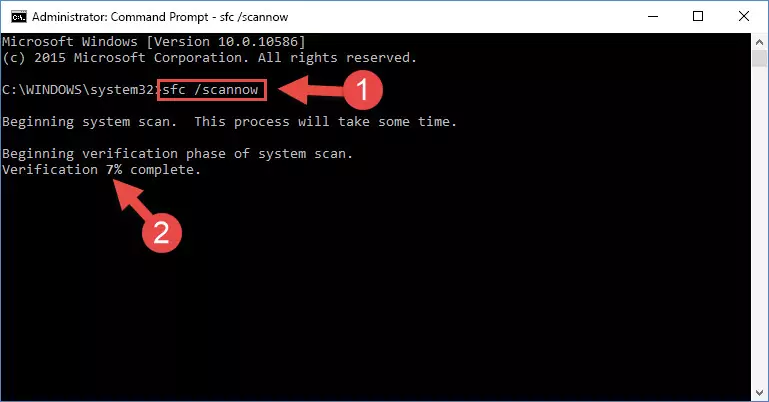
Method 5: Fixing the Tipp377.dll Error by Manually Updating Windows
Most of the time, softwares have been programmed to use the most recent dll files. If your operating system is not updated, these files cannot be provided and dll errors appear. So, we will try to solve the dll errors by updating the operating system.
Since the methods to update Windows versions are different from each other, we found it appropriate to prepare a separate article for each Windows version. You can get our update article that relates to your operating system version by using the links below.
Guides to Manually Update for All Windows Versions
Our Most Common Tipp377.dll Error Messages
The Tipp377.dll file being damaged or for any reason being deleted can cause softwares or Windows system tools (Windows Media Player, Paint, etc.) that use this file to produce an error. Below you can find a list of errors that can be received when the Tipp377.dll file is missing.
If you have come across one of these errors, you can download the Tipp377.dll file by clicking on the "Download" button on the top-left of this page. We explained to you how to use the file you'll download in the above sections of this writing. You can see the suggestions we gave on how to solve your problem by scrolling up on the page.
- "Tipp377.dll not found." error
- "The file Tipp377.dll is missing." error
- "Tipp377.dll access violation." error
- "Cannot register Tipp377.dll." error
- "Cannot find Tipp377.dll." error
- "This application failed to start because Tipp377.dll was not found. Re-installing the application may fix this problem." error
