- Download Price:
- Free
- Dll Description:
- Norton Internet Security Firewall Settings Engine
- Versions:
- Size:
- 0.32 MB
- Operating Systems:
- Developers:
- Directory:
- C
- Downloads:
- 629 times.
What is Ccfwsetg.dll?
The Ccfwsetg.dll file was developed by Symantec.
The Ccfwsetg.dll file is 0.32 MB. The download links are current and no negative feedback has been received by users. It has been downloaded 629 times since release.
Table of Contents
- What is Ccfwsetg.dll?
- Operating Systems That Can Use the Ccfwsetg.dll File
- All Versions of the Ccfwsetg.dll File
- How to Download Ccfwsetg.dll
- Methods for Solving Ccfwsetg.dll
- Method 1: Installing the Ccfwsetg.dll File to the Windows System Folder
- Method 2: Copying the Ccfwsetg.dll File to the Software File Folder
- Method 3: Doing a Clean Reinstall of the Software That Is Giving the Ccfwsetg.dll Error
- Method 4: Solving the Ccfwsetg.dll Error Using the Windows System File Checker
- Method 5: Fixing the Ccfwsetg.dll Errors by Manually Updating Windows
- Common Ccfwsetg.dll Errors
- Dll Files Similar to Ccfwsetg.dll
Operating Systems That Can Use the Ccfwsetg.dll File
All Versions of the Ccfwsetg.dll File
The last version of the Ccfwsetg.dll file is the 7.0.0.806 version.This dll file only has one version. There is no other version that can be downloaded.
- 7.0.0.806 - 32 Bit (x86) Download directly this version
How to Download Ccfwsetg.dll
- Click on the green-colored "Download" button on the top left side of the page.
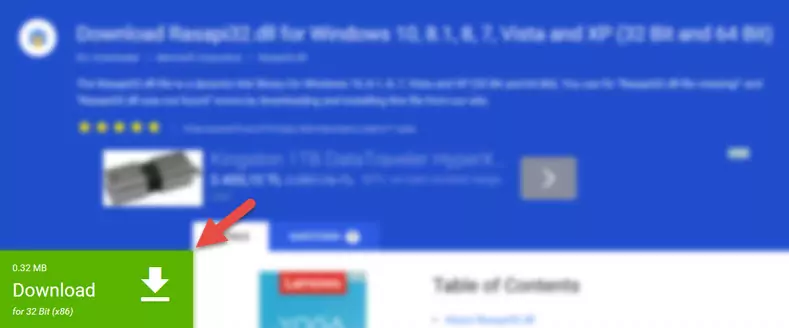
Step 1:Download process of the Ccfwsetg.dll file's - "After clicking the Download" button, wait for the download process to begin in the "Downloading" page that opens up. Depending on your Internet speed, the download process will begin in approximately 4 -5 seconds.
Methods for Solving Ccfwsetg.dll
ATTENTION! Before beginning the installation of the Ccfwsetg.dll file, you must download the file. If you don't know how to download the file or if you are having a problem while downloading, you can look at our download guide a few lines above.
Method 1: Installing the Ccfwsetg.dll File to the Windows System Folder
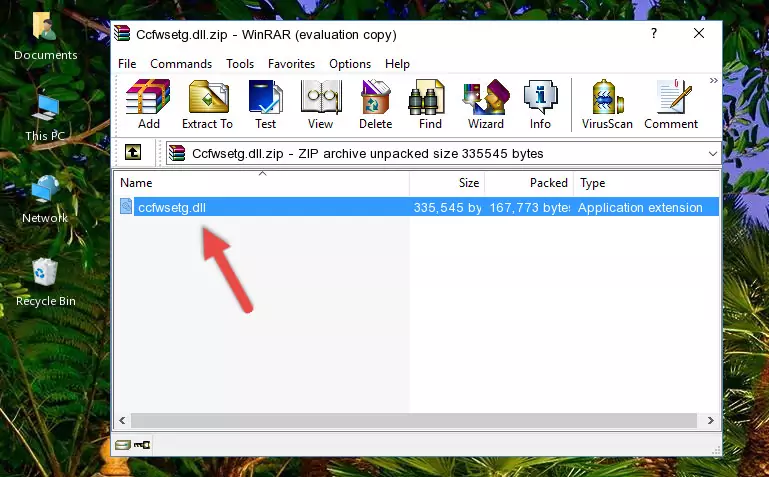
- The file you downloaded is a compressed file with the extension ".zip". This file cannot be installed. To be able to install it, first you need to extract the dll file from within it. So, first double-click the file with the ".zip" extension and open the file.
- You will see the file named "Ccfwsetg.dll" in the window that opens. This is the file you need to install. Click on the dll file with the left button of the mouse. By doing this, you select the file.
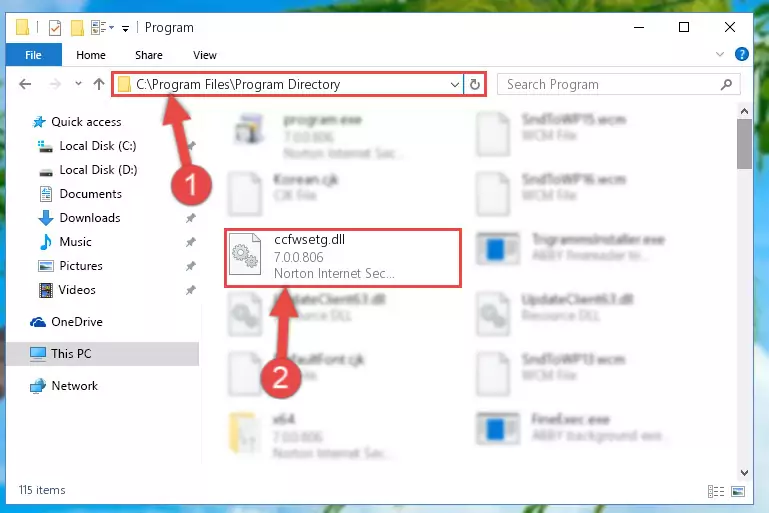
Step 2:Choosing the Ccfwsetg.dll file - Click on the "Extract To" button, which is marked in the picture. In order to do this, you will need the Winrar software. If you don't have the software, it can be found doing a quick search on the Internet and you can download it (The Winrar software is free).
- After clicking the "Extract to" button, a window where you can choose the location you want will open. Choose the "Desktop" location in this window and extract the dll file to the desktop by clicking the "Ok" button.
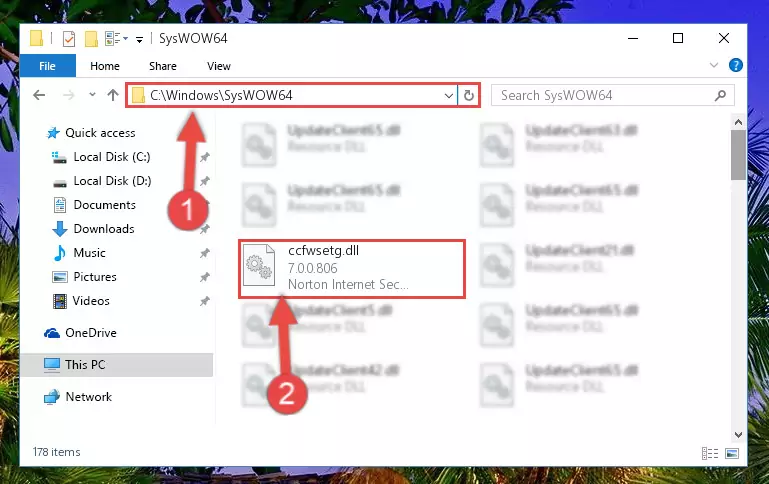
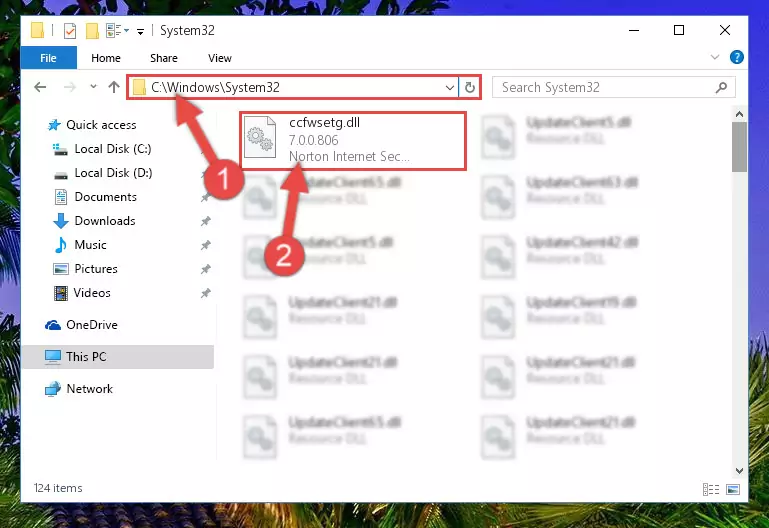
Step 3:Extracting the Ccfwsetg.dll file to the desktop - Copy the "Ccfwsetg.dll" file you extracted and paste it into the "C:\Windows\System32" folder.
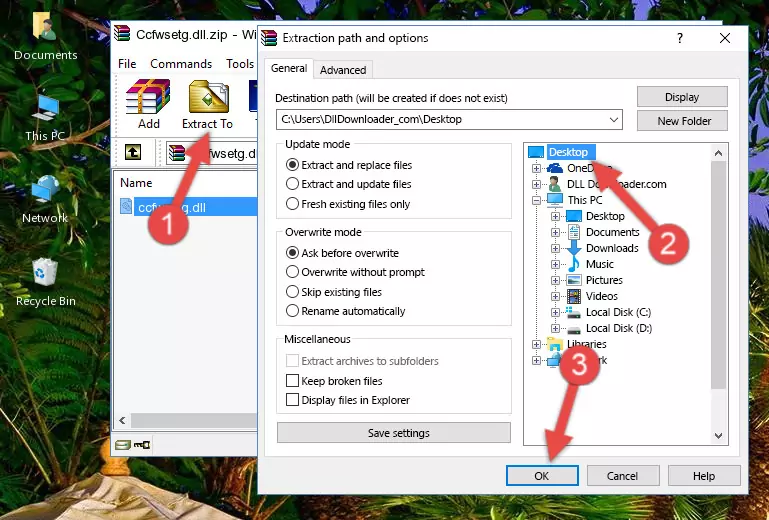
Step 3:Copying the Ccfwsetg.dll file into the Windows/System32 folder - If you are using a 64 Bit operating system, copy the "Ccfwsetg.dll" file and paste it into the "C:\Windows\sysWOW64" as well.
NOTE! On Windows operating systems with 64 Bit architecture, the dll file must be in both the "sysWOW64" folder as well as the "System32" folder. In other words, you must copy the "Ccfwsetg.dll" file into both folders.
Step 4:Pasting the Ccfwsetg.dll file into the Windows/sysWOW64 folder - In order to run the Command Line as an administrator, complete the following steps.
NOTE! In this explanation, we ran the Command Line on Windows 10. If you are using one of the Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP operating systems, you can use the same methods to run the Command Line as an administrator. Even though the pictures are taken from Windows 10, the processes are similar.
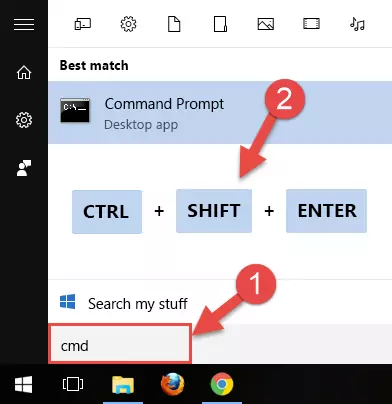
- First, open the Start Menu and before clicking anywhere, type "cmd" but do not press Enter.
- When you see the "Command Line" option among the search results, hit the "CTRL" + "SHIFT" + "ENTER" keys on your keyboard.
- A window will pop up asking, "Do you want to run this process?". Confirm it by clicking to "Yes" button.
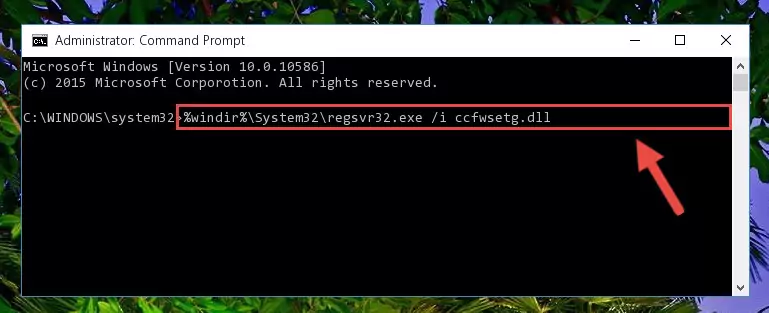
Step 5:Running the Command Line as an administrator - Let's copy the command below and paste it in the Command Line that comes up, then let's press Enter. This command deletes the Ccfwsetg.dll file's problematic registry in the Windows Registry Editor (The file that we copied to the System32 folder does not perform any action with the file, it just deletes the registry in the Windows Registry Editor. The file that we pasted into the System32 folder will not be damaged).
%windir%\System32\regsvr32.exe /u Ccfwsetg.dll
Step 6:Deleting the Ccfwsetg.dll file's problematic registry in the Windows Registry Editor - If the Windows you use has 64 Bit architecture, after running the command above, you must run the command below. This command will clean the broken registry of the Ccfwsetg.dll file from the 64 Bit architecture (The Cleaning process is only with registries in the Windows Registry Editor. In other words, the dll file that we pasted into the SysWoW64 folder will stay as it is).
%windir%\SysWoW64\regsvr32.exe /u Ccfwsetg.dll
Step 7:Uninstalling the broken registry of the Ccfwsetg.dll file from the Windows Registry Editor (for 64 Bit) - You must create a new registry for the dll file that you deleted from the registry editor. In order to do this, copy the command below and paste it into the Command Line and hit Enter.
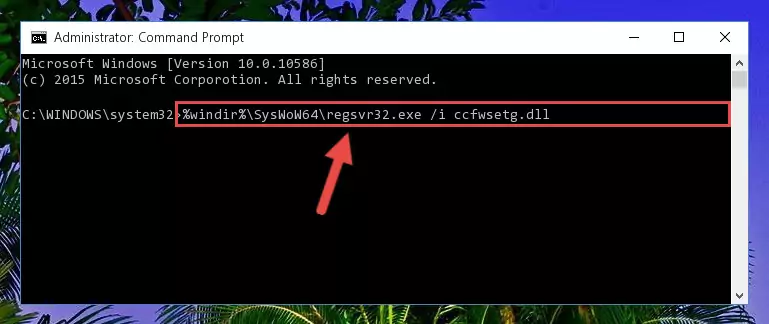
%windir%\System32\regsvr32.exe /i Ccfwsetg.dll
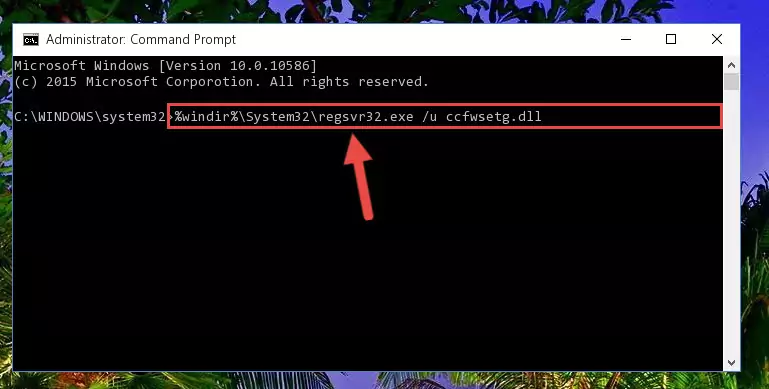
Step 8:Creating a new registry for the Ccfwsetg.dll file - If you are using a Windows with 64 Bit architecture, after running the previous command, you need to run the command below. By running this command, we will have created a clean registry for the Ccfwsetg.dll file (We deleted the damaged registry with the previous command).
%windir%\SysWoW64\regsvr32.exe /i Ccfwsetg.dll
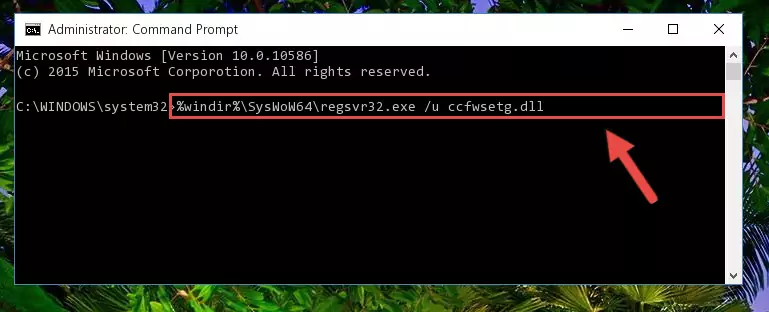
Step 9:Creating a clean registry for the Ccfwsetg.dll file (for 64 Bit) - If you did the processes in full, the installation should have finished successfully. If you received an error from the command line, you don't need to be anxious. Even if the Ccfwsetg.dll file was installed successfully, you can still receive error messages like these due to some incompatibilities. In order to test whether your dll problem was solved or not, try running the software giving the error message again. If the error is continuing, try the 2nd Method to solve this problem.
Method 2: Copying the Ccfwsetg.dll File to the Software File Folder
- First, you must find the installation folder of the software (the software giving the dll error) you are going to install the dll file to. In order to find this folder, "Right-Click > Properties" on the software's shortcut.
Step 1:Opening the software's shortcut properties window - Open the software file folder by clicking the Open File Location button in the "Properties" window that comes up.
Step 2:Finding the software's file folder - Copy the Ccfwsetg.dll file.
- Paste the dll file you copied into the software's file folder that we just opened.
Step 3:Pasting the Ccfwsetg.dll file into the software's file folder - When the dll file is moved to the software file folder, it means that the process is completed. Check to see if the problem was solved by running the software giving the error message again. If you are still receiving the error message, you can complete the 3rd Method as an alternative.
Method 3: Doing a Clean Reinstall of the Software That Is Giving the Ccfwsetg.dll Error
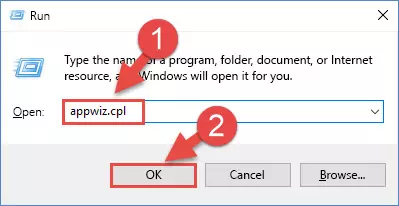
- Push the "Windows" + "R" keys at the same time to open the Run window. Type the command below into the Run window that opens up and hit Enter. This process will open the "Programs and Features" window.
appwiz.cpl
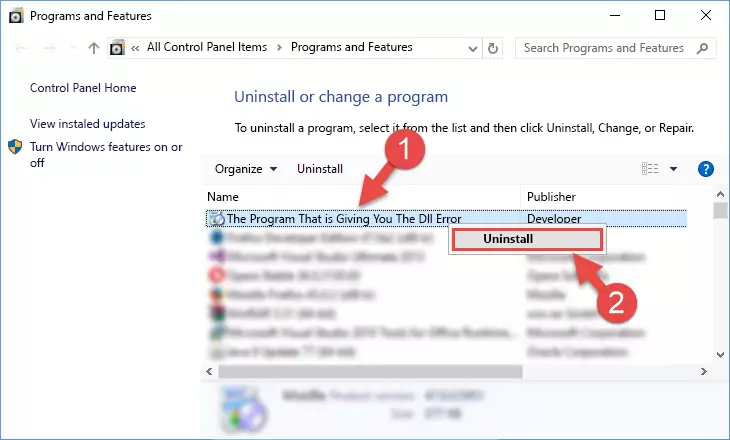
Step 1:Opening the Programs and Features window using the appwiz.cpl command - The softwares listed in the Programs and Features window that opens up are the softwares installed on your computer. Find the software that gives you the dll error and run the "Right-Click > Uninstall" command on this software.
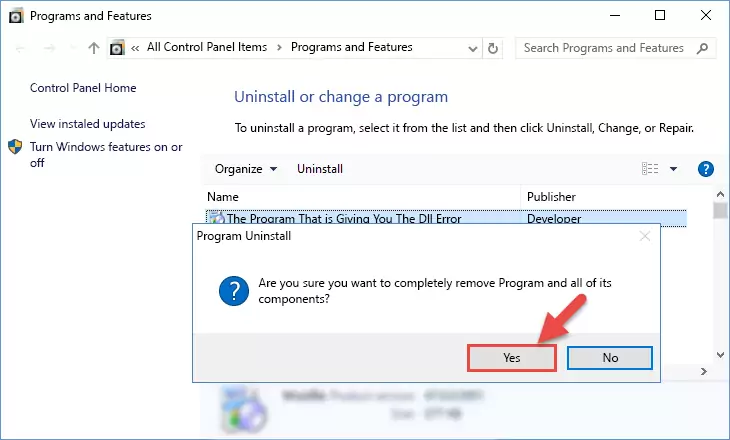
Step 2:Uninstalling the software from your computer - Following the instructions that come up, uninstall the software from your computer and restart your computer.
Step 3:Following the verification and instructions for the software uninstall process - After restarting your computer, reinstall the software.
- You may be able to solve the dll error you are experiencing by using this method. If the error messages are continuing despite all these processes, we may have a problem deriving from Windows. To solve dll errors deriving from Windows, you need to complete the 4th Method and the 5th Method in the list.
Method 4: Solving the Ccfwsetg.dll Error Using the Windows System File Checker
- In order to run the Command Line as an administrator, complete the following steps.
NOTE! In this explanation, we ran the Command Line on Windows 10. If you are using one of the Windows 8.1, Windows 8, Windows 7, Windows Vista or Windows XP operating systems, you can use the same methods to run the Command Line as an administrator. Even though the pictures are taken from Windows 10, the processes are similar.
- First, open the Start Menu and before clicking anywhere, type "cmd" but do not press Enter.
- When you see the "Command Line" option among the search results, hit the "CTRL" + "SHIFT" + "ENTER" keys on your keyboard.
- A window will pop up asking, "Do you want to run this process?". Confirm it by clicking to "Yes" button.

Step 1:Running the Command Line as an administrator - Paste the command in the line below into the Command Line that opens up and press Enter key.
sfc /scannow
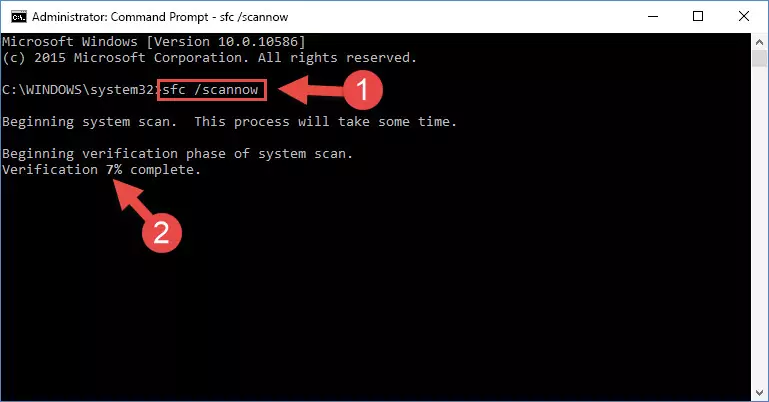
Step 2:solving Windows system errors using the sfc /scannow command - The scan and repair process can take some time depending on your hardware and amount of system errors. Wait for the process to complete. After the repair process finishes, try running the software that is giving you're the error.
Method 5: Fixing the Ccfwsetg.dll Errors by Manually Updating Windows
Some softwares require updated dll files from the operating system. If your operating system is not updated, this requirement is not met and you will receive dll errors. Because of this, updating your operating system may solve the dll errors you are experiencing.
Most of the time, operating systems are automatically updated. However, in some situations, the automatic updates may not work. For situations like this, you may need to check for updates manually.
For every Windows version, the process of manually checking for updates is different. Because of this, we prepared a special guide for each Windows version. You can get our guides to manually check for updates based on the Windows version you use through the links below.
Explanations on Updating Windows Manually
Common Ccfwsetg.dll Errors
When the Ccfwsetg.dll file is damaged or missing, the softwares that use this dll file will give an error. Not only external softwares, but also basic Windows softwares and tools use dll files. Because of this, when you try to use basic Windows softwares and tools (For example, when you open Internet Explorer or Windows Media Player), you may come across errors. We have listed the most common Ccfwsetg.dll errors below.
You will get rid of the errors listed below when you download the Ccfwsetg.dll file from DLL Downloader.com and follow the steps we explained above.
- "Ccfwsetg.dll not found." error
- "The file Ccfwsetg.dll is missing." error
- "Ccfwsetg.dll access violation." error
- "Cannot register Ccfwsetg.dll." error
- "Cannot find Ccfwsetg.dll." error
- "This application failed to start because Ccfwsetg.dll was not found. Re-installing the application may fix this problem." error
